
2021.08.21 - [Programming/Machine Learning] - Scoring Feature Importance by Information Gain
목차
Information Gain(IG)은 어떤 조건으로 데이터를 분류할 때 엔트로피가 얼마나 감소하는지를 측정하는 양이다. 여러 입력 데이터(input feature)를 통해 원하는 어떤 출력 값(output target)을 예측하고 싶을 때, 각각의 feature가 독립적으로 target을 얼마나 정확하게 예측할 수 있는지를 평가하는 지표로 활용된다. 대표적인 예는 Decision Tree를 구성할 때 노드들의 feature를 할당하는 것이다.
정보학 분야에서 엔트로피는 정보를 수치화하는 양으로 Shannon 엔트로피를 이용한다.
$$ H = -\sum_{i}^{C}p_i\log_2 p_i $$
여기에서 $C$는 클래스이고 $p_i$는 클래스 $i$를 뽑을 확률이다. 밑이 2인 로그의 이유는 정보의 가장 기본 단위인 0과 1의 bitwise계산에서 값을 규격화하기 위함이다. 따라서 엔트로피는 0과 1 사이의 값을 갖는다.
간단한 이진 분류(Binary classification)의 경우에는 다음과 같이 엔트로피를 계산한다.
$$ H = - p(0)\log_2(p(0)) - p(1)\log_2(p(1)) $$
여기에서 $p(0)$와 $p(1)$은 두 클래스의 상대적 빈도수이다. 만약 두 클래스의 비중이 50:50으로 구성되어 있다면 엔트로피는 1이 된다. 이는 둘 중에 어떤 클래스가 뽑힐지에 대한 정보 획득이 아주 낮은 것을 의미한다. 반면, 100:0의 비율로 주어지면 엔트로피는 0으로 최소가 되어 샘플링이 아주 예측 가능해진다.
이 포스팅은 간단한 두 개의 예제를 통해 엔트로피와 IG를 수기와 코딩으로 계산해보며 그 개념과 적용에 대한 이해를 위한 목적으로 쓰였다.
예제 1 (Binary Classification)
첫 번째 예제는 아래와 같이 o, x 두 가지 종류로 이루어진 2차원 데이터 분포를 다루는 것이다. 목표는 이 분포가 x축의 어떤 값에 의해 두 그룹으로 분류 되었을 때 엔트로피의 변화와 IG값을 구하는 것이다.
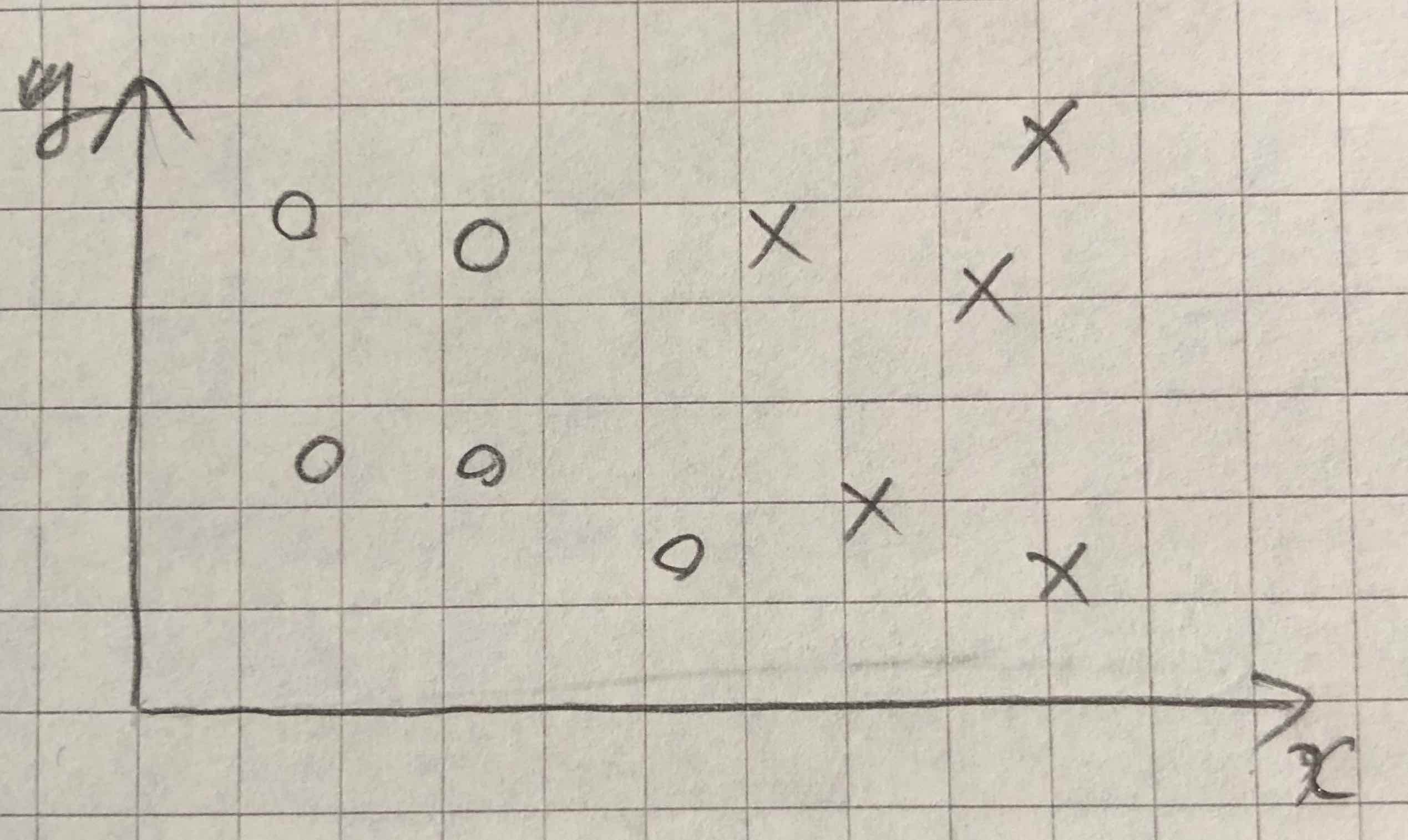
먼저 나누기 전의 엔트로피를 계산한다. 이때 o:x = 1:1이다.
$$ \begin{align} H_{before} &= -P(o)\log_2(P(o)) -P(\mathrm{x})\log_2(P(\mathrm{x})) \\ &= -1/2\log_2(1/2) -1/2\log_2(1/2) \\ &= 1 \end{align}$$
예측한대로 엔트로피는 1이 나왔다. 이것은 o와 x가 같은 개수가 있기 때문에 불순도(impurity)가 아주 높다는 것을 의미한다.
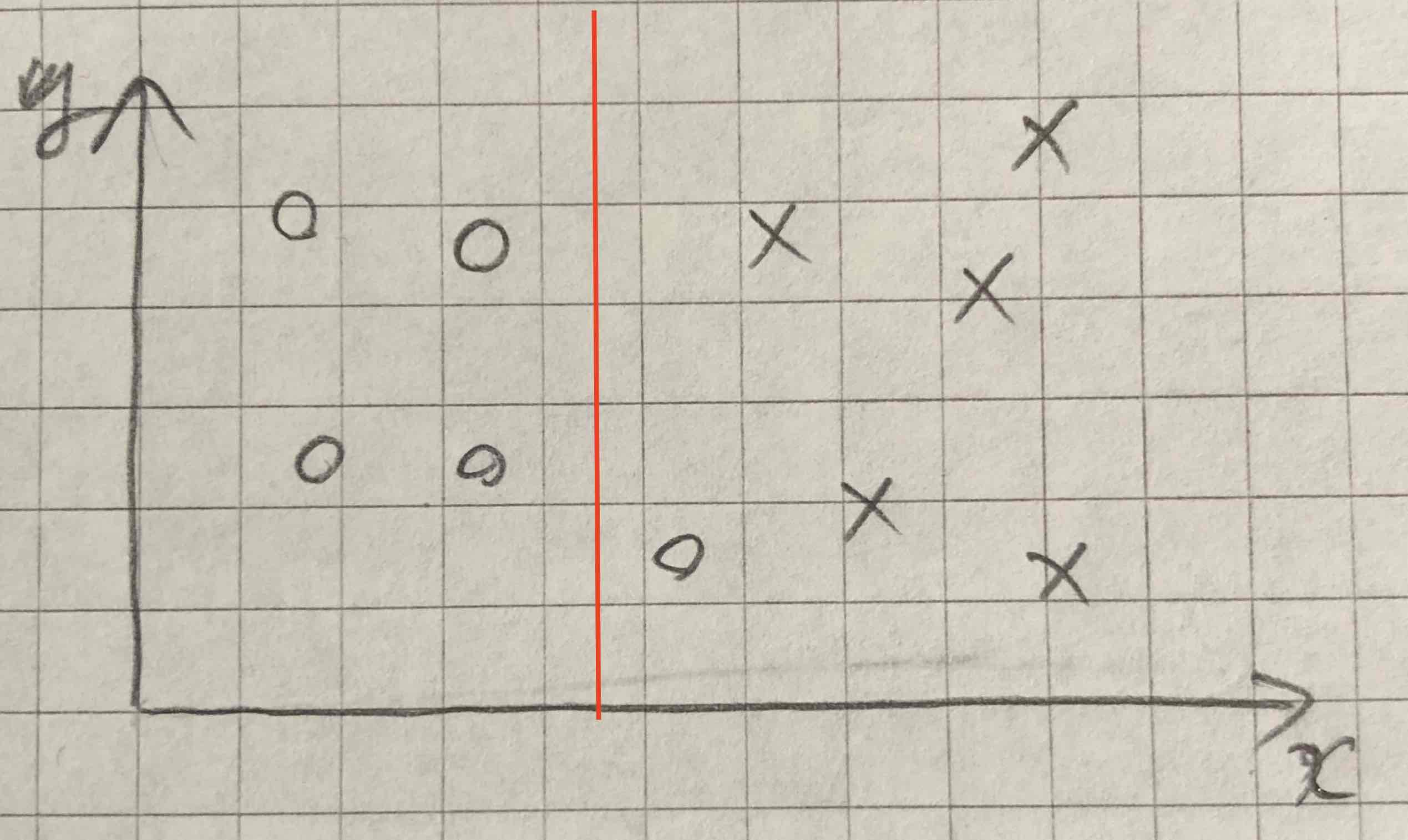
그림 1의 오른쪽과 같이 데이터를 나눈 후 엔트로피의 변화를 살펴보자. 빨간선을 기준으로 왼쪽과 오른쪽 파티션의 엔트로피를 따로 계산해야 한다.
- 왼쪽 파티션:
여기에는 o만 있다. 따라서 $H_{left}=0$ 이다.
- 오른쪽 파티션:
여기에는 5개의 x와 1개의 o가 있다. $P(\mathrm{x}) = 5/6, P(o) = 1/6$이다. 엔트로피는 다음과 같다.
$$H_{right} = -5/6\log_2(5/6) - 1/6\log_2(1/6) = 0.65$$
이 두 파티션의 엔트로피를 가중치를 고려해 합하여 전체 엔트로피 $H_{split}$를 구한다.
$$ H_{split} = (4/10)H_{left} + (6/10)H_{right} = (4/10)*0 + (6/10)*0.65 = 0.39 $$
이제는 information gain(IG)를 얻을 수 있다.
$$IG = H_{before} - H_{split} = 0.61$$
비교적 높은 값이라고 할 수 있다.
빨간선을 옮기면 데이터가 다르게 분류될 것이고 이에 따라 $H_{split}$과 IG가 변할 것이다. 만약, o, x가 서로 섞이지 않고 분류되면 IG=1이 될 것이다. 반면, 10개의 o, x가 모두 포함되도록 분류했다면 H_before=H_split이 되어 IG=0이 될 것이다.
예제 2 (Feature selection)
두 번째 예제는 여러 input feature들과 한 개의 target을 포함하는 데이터를 다뤄 보도록 하겠다. 이 예제에 대해서는 IG를 수기와 파이썬 코딩으로 계산해 보도록 하겠다.
먼저 필요한 라이브러리를 import 한다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as st
pandas로 csv 포맷의 간단한 데이터를 읽는다.
df = pd.read_csv("self_driving_car.csv")
df.columns=['Grade', 'Bumpiness', 'Speed Limit', 'Speed']
display(df)
위의 데이터에서 Grade, Bumpiness, Speed Limit이 input feature이고 Speed가 예측할 target이다. speed를 예측하기 위한 decision tree를 만든다고 할 때, 각 input feature들의 예측능력을 IG 계산으로 평가해 보는 것이다.
아래 그림과 같은 세 가지 분류가 가능하다.
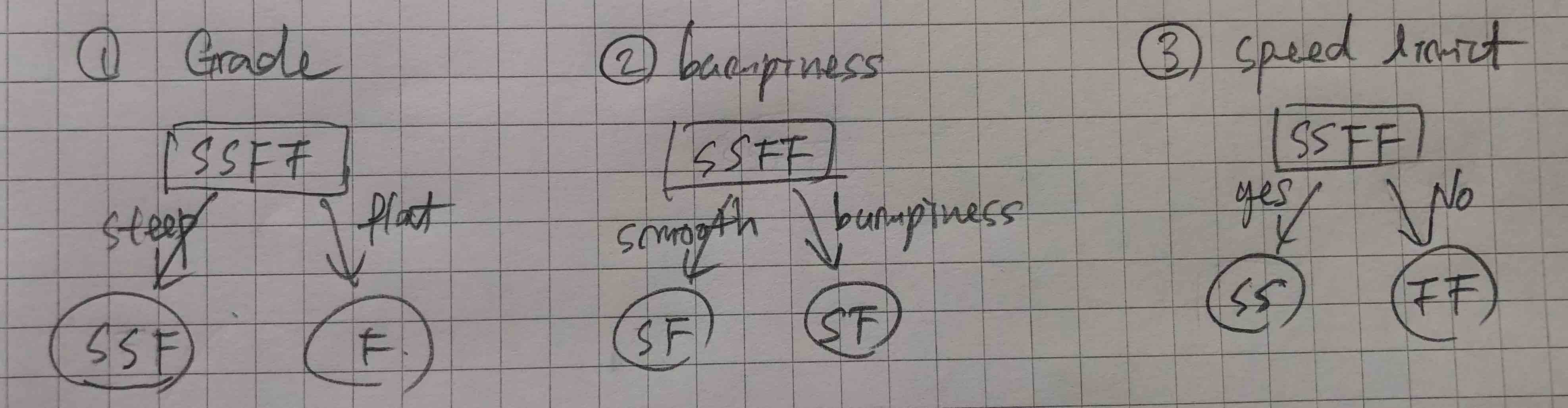
나누기 전의 Speed는 Slow와 Fast 각각 두 개씩 있다 (SSFF). 이것을 Grade는 SSF와 F로 분류한다. 반면 bumpiness는 SF/SF로 분류하고, Speed Limit은 SS/FF로 분류한다. 이제 각각의 분류에 대한 IG, 즉 IG(Grade), IG(bumpiness), IG(Speed Limit) 세 값을 구하는 것이다.
$$ IG(feature) = H_{before} - H_{split \, by \, feature} $$
H_before 계산
먼저 분류하기 전 target 변수의 엔트로피를 구한다. Speed 값의 각 클래스의 빈도수를 측정한다. 위의 표에서 보듯이 S/F가 2개씩 있다.
target = {}
for c in df.Speed:
if c not in target:
target[c] = 1
else:
target[c] +=1
print(target)
이것의 엔트로피는 1이 된다.
entropy_before = st.entropy(list(target.values()), base=2)
print(entropy_before)
# output
# 1.0
Information Gain 계산
이제 세 개의 각 feature로 Speed의 클래스를 분류할 때 엔트로피의 변화가 어떻게 되는지 살펴보자. 코딩 전에 먼저 손으로 계산해보자.
1. Grade -> SSF/F
$H(SSF) = - 2/3\log_2(2/3) -1/3\log_2(1/3) = 0.92$
$H(F) = 0$
$H_{split\,by \,Grade} = 3/4*H(SSF) + 1/4*H(F) = 0.69 $
$IG(Grade) = H_{before} - H_{split \,by \,Grade} = 1 - 0.69 = 0.31 $
2. Bumpiness -> SF/SF
$H(SF) = 1$
$H_{split\,by \,Bumpiness} = 2/4*H(SF) + 2/4*H(SF) = 1$
$IG(Bumpiness) = H_{before} - H_{split \, by \, Bumpiness} = 1 - 1 = 0 $
3. Speed Limit -> SS/FF
$H(SS) = H(FF) = 0$
$H_{split \, by \, Speed \, Limit}= 0$
$IG(Speed \,Limit) = H_{before} - H_{split \, by \, Speed \, Limit} = 1$
예측한대로 Speed Limit의 IG가 가장 크게 나왔다. 그 이유는 Speed가 Speed Limit에 의해 SS/FF 두 클래스로 정확하게 분류되었기 때문이다. 따라서 Decision tree를 만들 때 꼭대기에 위치하는 root 노드에는 Speed Limit을 할당하는 것이 다른 두 feature보다 예측 모델의 정확도를 더 높일 수 있게 된다.
Simple Python Coding
위해서 구한 값들을 코딩으로 얻어보자.
def weightedEntropy(feature):
df2 = df[['Speed',feature]].groupby(feature).agg({'Speed': lambda x: list(x)})
df2['Count'] = [len(i) for i in df2['Speed']]
df2.reset_index([feature], inplace=True)
print("")
print("Speed grouped by %s"%feature)
display(df2)
TotalCount = sum(df2.Count)
weightedEntropy = 0
for i in range(df2.shape[0]):
sd = df2.iloc[i].Speed
cnt = df2.iloc[i].Count
weightedEntropy += st.entropy(list(Counter(sd).values()), base=2)*cnt/TotalCount
return weightedEntropyIG={}
# df.columns=['Grade', 'Bumpiness', 'Speed Limit', 'Speed']
for feature in df.columns[:-1]:
IG[feature] = entropy_before - weightedEntropy(feature)
print(IG)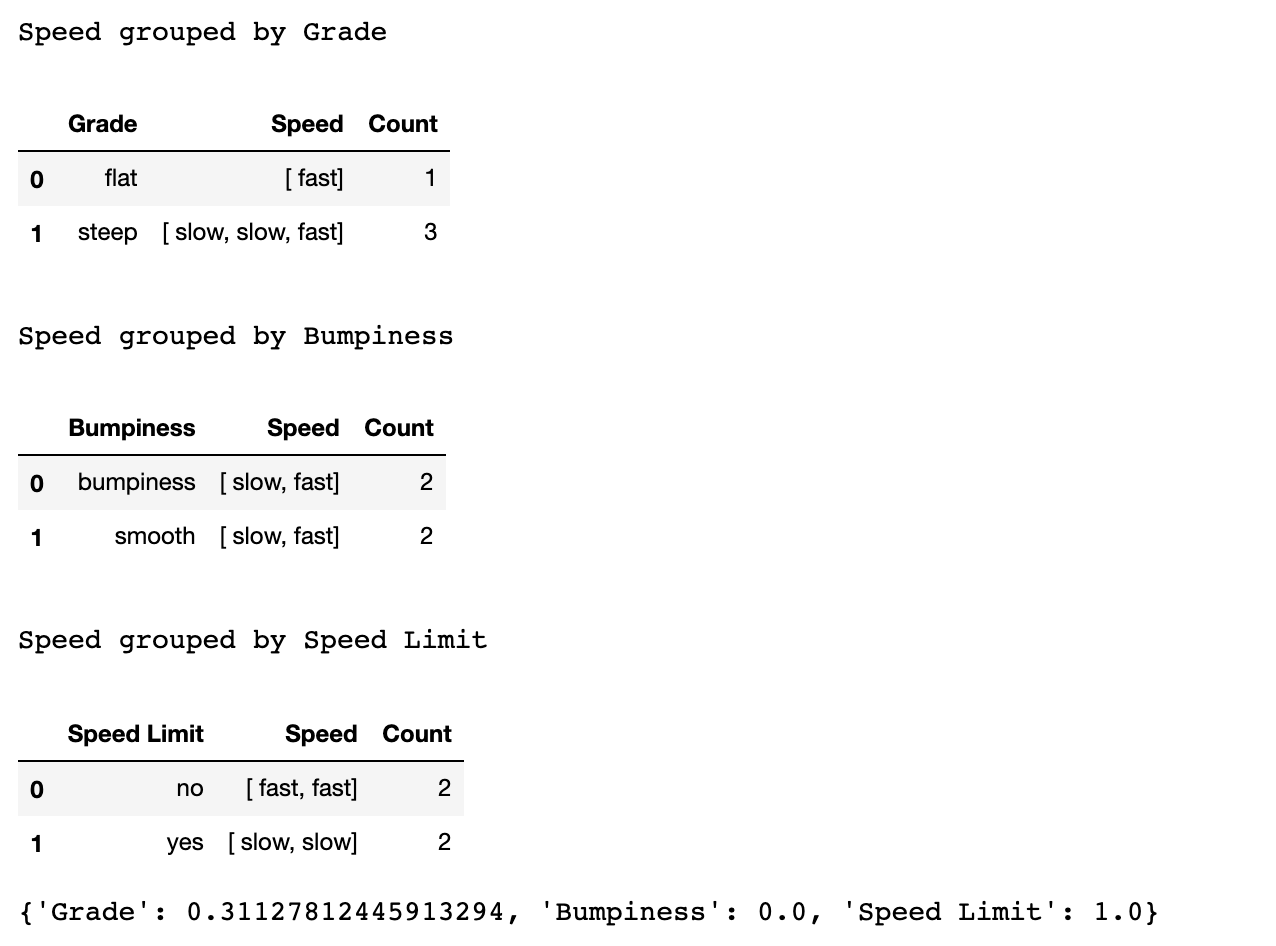
예측대로 나온 것을 확인할 수 있다.
결과를 bar 그래프로 그려본다.
from collections import OrderedDict
plt.rcParams.update({'font.size': 15})
SortedIG = OrderedDict(sorted(IG.items(),key=lambda kv: kv[1], reverse=True))
keys = SortedIG.keys()
values = SortedIG.values()
plt.figure(figsize=(10,5))
plt.bar(keys, values)
plt.ylabel('information gain',fontsize=15)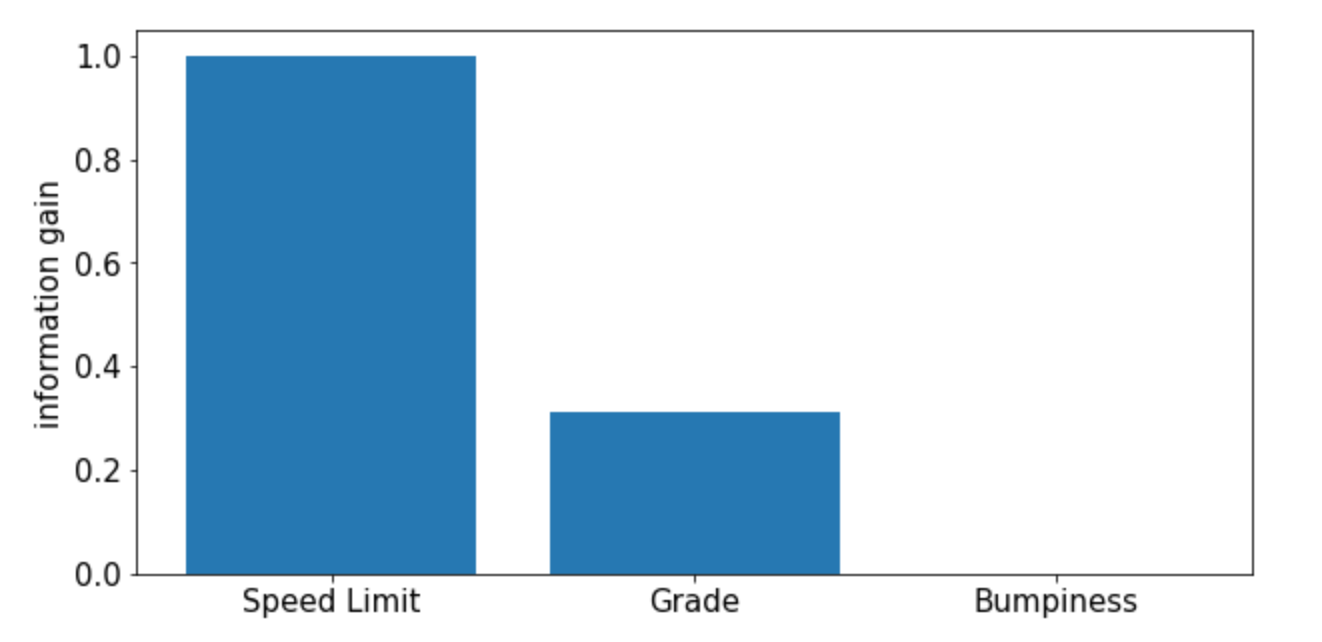
마치며
비록 간단한 예제이지만 Information Gain과 Information Entropy에 대한 이해를 하는데 큰 도움이 되어 정리해 보았다. 이것을 더 큰 실제 데이터셋에 적용해 볼 수 있겠다. 여기에서는 두 개의 클래스가 있는 경우만을 보았지만, 실제로는 target값에 여러 개의 클래스가 섞여 있을 수 있다. 이때는 로그의 밑을 클래스의 개수만큼 정해주면 규격화하는 데는 문제가 없다. 하지만 클래스들의 분포가 균일하지 않는다면 $H_{before}$가 낮은 값을 갖게 되어 IG의 값이 아주 작아지게 될 수 있어 rescaling을 고려해야 할 수도 있다. 이것은 나중에 살펴보도록 하겠다.
References
- https://victorzhou.com/blog/information-gain/
- https://machinelearningmastery.com/information-gain-and-mutual-information/
- https://medium.com/coinmonks/what-is-entropy-and-why-information-gain-is-matter-4e85d46d2f01
'Programming > Machine Learning' 카테고리의 다른 글
| 1D Convolutional Neural Network 이해하기 (CNN in numpy & keras) (0) | 2021.08.27 |
|---|---|
| Feature Importance with Information Gain (0) | 2021.08.21 |
| Seaborn boxplot으로 five-number summary 이해하기 (0) | 2021.05.03 |
| Tensorflow: regression 기본 예제 (연료 효율성 예측) (0) | 2020.11.14 |
| [Tensorflow] House Price 예측 모델 (keras) (feat. 정확도 향상) (0) | 2020.10.30 |




댓글