[OpenCV] Image Edge Enhancement: 라플라스 연산자 (Laplace Operator)-파이썬 코드 포함

[OpenCV] 라플라스 연산자 (Laplace Operator)

이미지 처리에서 sharpening이라고 하는 즉 선명도를 증가시키는 방법이 몇 가지 있습니다. 가장 대표적인  방법으로 다음의 4가지를 뽑을 수 있고, 이 포스팅에선 라플라스 연산자에 대해서 보도록 하겠습니다. 

 

1. Laplace operator 
2. Difference of Gaussians (DoG)
3. Unsharp Filter 

2020/10/27 - [분류 전체보기] - [OpenCV] 이미지 경계선 강화: Unsharped 필터 - 파이썬 코드 포함

2020/10/27 - [OpenCV] - [OpenCV] 이미지 경계선 강화: DoG - 파이썬 코드 포함

Laplace operator  

라플라스 연산자는 주로 edge를 감지하거나 동작을 잡아내는데 사용된다. 이것은 공간에 대한 2차 미분으로 정의된다. 여기에서 $ f(x,y)$는 2차원 이미지의 픽셀 값의 함수이다.

 

$$ \mathbf{L} = \nabla^2 f(x,y) = \left[\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} \right] f(x,y) \tag{1}$$

 

아래 왼쪽 그림에서 보이는 바와 같이 edge에서는 대개 픽셀 값이 많이 변하게 된다. 이것에 대한 1차 미분으로 가장 급격하게 변하는 부분을 잡아 낼 수 있다. 

2차 미분을 하면 아래와 같이 변곡점에서 0이 되는 지점을 찾아낸다. 이것을 바로 픽셀값이 급격히 바뀌는 즉 이미지 내의 edge로 간주하고, edge 주변으로 픽셀 값이 역시 크게 변하는 것을 알 수 있다. 

 

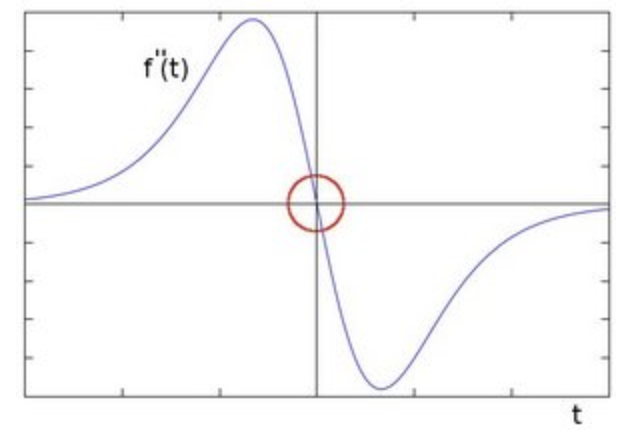
실제 이미지 처리에서는 불연속적으로 근사된 라플라스 필터를 이미지에 합성곱으로 적용한다. 여기에 사용되는 라플라스 필터는 이미지보다 크기가 훨씬 작다. 주로 3x3의 행렬이 쓰인다. 다음의 세 종류가 보통이다. 

세 종류의 digitized 라플라시안 필터

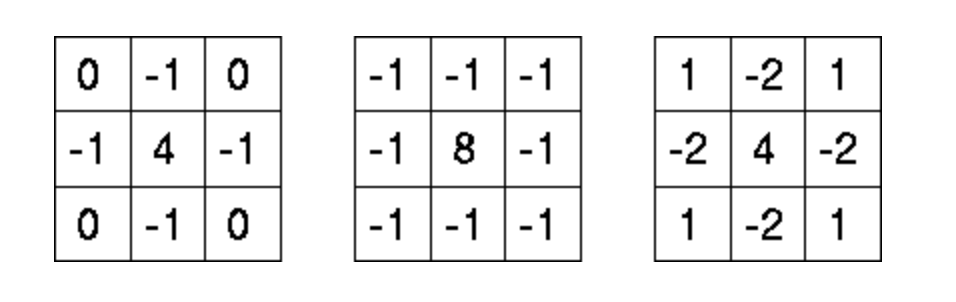
아래의 코드는 파이썬으로 이미지를 읽고 라플라스와 가우시안 필터를 적용해 본 것이다. 각 필터링에 두가지 방법, OpenCV이용한 것과 직접 짠 코드, 를 사용하여 결과를 비교하였다. 

 

 

다음과 같이 실행해 볼 수 있으며  아래 세 그림으로 결과를 볼 수 있다. 

 

(왼쪽) 원본 이미지  (가운데) 라플라시안 필터링 이미지  (오른쪽) 둘의 합성 이미지 

위의 오른쪽 그림에서 edge는 뚜렷해진 것을 확인할 수 있지만, 전체적으로 노이즈가 증가했다. 이것은 라플라스 필터링이 노이즈에 민감하게 작용하기 때문이다. 이것은 보완하는 다른 알고리즘은 Unsharp filter를 사용하는 것이고, 이것은 이어지는 포스팅에서 살펴보도록 하겠습니다.

 

 

마지막으로 직접 짠 코드로 적용한 Laplacian 와 Gaussian filter결과 입니다. 아래와 같이 실행하여 결과를 확인할 수 있습니다. 

Laplacian filtered image 

 

Gaussian blurred image 

 

참고 링크 및 이미지 출처

1. Unsharp Filter

2. OpenCV:Laplace Operator